Nature Of Mathematics Education Pdf
- Editorial
- Open Access
- Published:
Problematizing teaching and learning mathematics as "given" in STEM education
International Journal of STEM Education volume 6, Article number:44 (2019) Cite this article
-
42k Accesses
-
24 Citations
-
8 Altmetric
-
Metrics details
Abstract
Mathematics is fundamental for many professions, especially science, technology, and engineering. Yet, mathematics is often perceived as difficult and many students leave disciplines in science, technology, engineering, and mathematics (STEM) as a result, closing doors to scientific, engineering, and technological careers. In this editorial, we argue that how mathematics is traditionally viewed as "given" or "fixed" for students' expected acquisition alienates many students and needs to be problematized. We propose an alternative approach to changes in mathematics education and show how the alternative also applies to STEM education.
Introduction
Mathematics is commonly perceived to be difficult (e.g., Fritz et al. 2019). Moreover, many believe "it is ok—not everyone can be good at math" (Rattan et al. 2012). With such perceptions, many students stop studying mathematics soon after it is no longer required of them. Giving up learning mathematics may seem acceptable to those who see mathematics as "optional," but it is deeply problematic for society as a whole. Mathematics is a gateway to many scientific and technological fields. Leaving it limits students' opportunities to learn a range of important subjects, thus limiting their future job opportunities and depriving society of a potential pool of quantitatively literate citizens. This situation needs to be changed, especially as we prepare students for the continuously increasing demand for quantitative and computational literacy over the twenty-first century (e.g., Committee on STEM Education 2018).
The goal of this editorial is to re-frame issues of change in mathematics education, with connections to science, technology, engineering, and mathematics (STEM) education. We are hardly the first to call for such changes; the history of mathematics and philosophy has seen ongoing changes in conceptualization of the discipline, and there have been numerous changes in the past century alone (Schoenfeld 2001). Yet changes in practice of how mathematics is viewed, taught, and learned have fallen far short of espoused aspirations. While there has been an increased focus on the processes and practices of mathematics (e.g., problem solving) over the past half century, the vast majority of the emphasis is still on what content should be presented to students. It is thus not surprising that significant progress has not been made.
We propose a two-fold reframing. The first shift is to re-emphasize the nature of mathematics—indeed, all of STEM—as a sense-making activity. Mathematics is typically conceptualized and presented as a body of content to be learned and processes to be engaged in, which can be seen in both the NCTM Standards volumes and the Common Core Standards. Alternatively, we believe that all of the mathematics studied in K-12 can be viewed as the codification of experiences of both making sense and sense making through various practices including problem solving, reasoning, communicating, and mathematical modeling, and that students can and should experience it that way. Indeed, much of the inductive part of mathematics has been lost, and the deductive part is often presented as rote procedures rather than a form of sense making. If we arrange for students to have the right experiences, the formal mathematics can serve to organize and systematize those experiences.
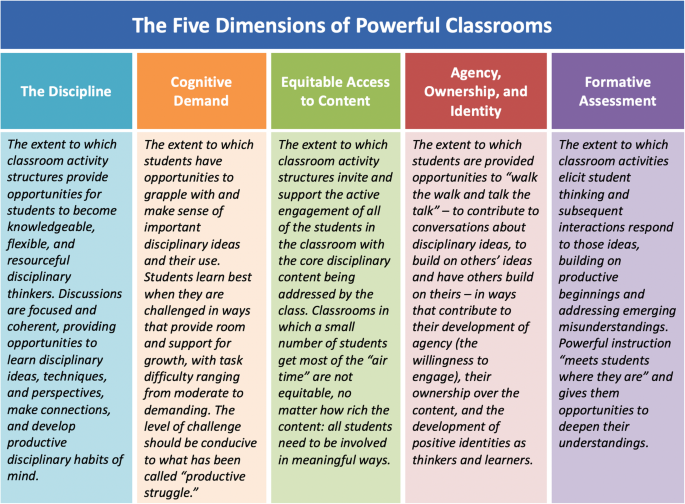
The second shift is suggested by the first, with specific attention to classroom instruction. Whether mathematics or STEM, the main focus of most instruction has been on the content and practices of the discipline, and what the teacher should do in order to make it accessible to students. Instead, we urge that the main focus should be on the student's experience of the discipline – on the affordances the environment provides the student for disciplinary sense making. We will introduce the Teaching for Robust Understanding (TRU) Framework, which can be used to problematize instruction and guide needed reframing. The first dimension of TRU (The Discipline) focuses on the re-framing discussed above: is the content conceptualized as something rich and connected that can be experienced and codified in meaningful ways? The second dimension (Cognitive Demand) examines opportunities students have to do that kind of sense-making and codification. The third (Equitable Access to Content) examines who has such opportunities: is there equitable access to the core ideas? Dimension 4 (Agency, Ownership, and Identity) asks, do students encounter the discipline in ways that enable them to see themselves as sense makers, building both agency and positive disciplinary identities? Finally, dimension 5 (Formative Assessment) asks, does instruction routinely use formative assessment, allowing student thinking to become public so that instruction can be adjusted accordingly?
We begin with a historical background, briefly discussing different views regarding the nature of mathematics. We then problematize traditional approaches to mathematics teaching and learning. Finally, we discuss possible changes in the context of STEM education.
Knowing the background: the development of conceptions about the nature of mathematics
The scholarly understanding of the nature of mathematics has evolved over its long history (e.g., Devlin 2012; Dossey 1992). Explicit discussions regarding the nature of mathematics took place among Greek mathematicians from 500 BC to 300 AD (see, https://en.wikipedia.org/wiki/Greek_mathematics). In contrast to the primarily utilitarian approaches that preceded them, the Greeks pioneered the study of mathematics for its own sake and pursued the development and use of generalized mathematical theories and proofs, especially in geometry and measurement (Boyer 1991). Different perspectives about the nature of mathematics were gradually developed during that time. Plato perceived the study of mathematics as pursuing the truth that exists in external world beyond people's mind. Mathematics was treated as a body of knowledge, in the ideal forms, that exists on its own, which human's mind may or may not sense. Aristotle, Plato's student, believed that mathematicians constructed mathematical ideas as a result of the idealization of their experience with objects (Dossey 1992). In this perspective, Aristotle emphasized logical reasoning and empirical realization of mathematical objects that are accessible to the human senses. The two schools of thought that evolved from Plato's and Aristotle's contrasting conceptions of the nature of mathematics have had important implications for the ensuing development of mathematics as a discipline, and for mathematics education.
Several more schools of thought were developed as mathematicians tackled new problems in mathematics (Dossey 1992). Davis and Hersh (1980) provides an entertaining and informative account of these developments. Three major schools of thought in the early 1900s dealt with paradoxes in the real number system and the theory of sets: (1) logicism, as an outgrowth of the Platonic school, accepts the external existence of mathematics and emphasizes the form rather than the interpretation in a specific setting; (2) intuitionism, as influenced by Aristotle's ideas, only accepts the mathematics to be developed from the natural numbers forward via "valid" patterns of mental reasoning (not empirical realization in Aristotle's thought); and (3) formalism, also aligned with Aristotle's ideas, builds mathematics upon the formal axiomatic structures to free mathematics from contradictions. These three schools of thought are similar in that they view the contents of mathematics as products, but they differ in whether products are viewed as pre-existing or created through experience. The development of these three schools of thought illustrates that the view of mathematics as products has its long history in mathematics.
With the gradual development of school mathematics since 1900s (Stanic and Kilpatrick 1992), the conception of the nature of mathematics has increasingly received attention from mathematics educators. Which notion of mathematics mathematics education adopts and uses has a direct and strong impact on the way of school mathematics being presented and approached in education. Although the history of school mathematics is relatively short in comparison with mathematics itself, we can find ample examples about the influence of different views of mathematics on curriculum and classroom instruction in the USA and other education systems (e.g., Dossey et al. 2016; Li and Lappan 2014; Li, Silver, and Li 2014; Stanic and Kilpatrick 1992). For instance, the "New Math" movement of 1950s and 1960s used the formalism school of thought as the core of reform efforts. The content was presented in a structural format, using the set theoretic language and conceptions. But the result was not a successful progression toward a school mathematics that is best for students and teachers (e.g., Kline 1973). Alternatively, Dossey (1992), in his review of the nature of mathematics, identified and selected scholars' works and ideas applicable to both professional mathematicians and mathematics educators (e.g., Davis and Hersh 1980; Hersh 1986; Tymoczko 1986). Those scholars' ideas rested on what professional mathematicians do, not what mathematicians think about what mathematics is. Dossey (1992) specifically cited Hersh (1986) to emphasize mathematics is about ideas and should be accepted as a human activity, not strictly governed by any one school of thought.
Devlin (2000) argued that mathematics is not a single entity but has four different faces: (1) computation, formal reasoning, and problem solving; (2) a way of knowing; (3) a creative medium; and (4) applications. Further, he contended school mathematics typically focuses on the first face, makes some reference to the fourth face, but pays almost no attention to the other two faces. His conception of mathematics assembles ideas from the history of mathematics and observes mathematical activities occurring across different settings.
Our brief review shows that the nature of mathematics can be understood as having different faces, rather than being governed by any single school of thought. At the same time, the ideas of Plato and Aristotle continue to influence the ways that mathematicians, mathematics educators, and the general public perceive mathematics. Despite nearly a half century of process-oriented research (see below), let alone Pólya's work on problem solving, mathematics is still perceived of largely as products—a body of knowledge as highlighted in the three schools (logicist, intuitionist, formalist) of thought, rather than ideas that call for active thinking and creation. The evolving conceptions about the nature of mathematics in history suggests there is room for us to decide how mathematics can be perceived, rather than being bounded by a pre-occupied notion of mathematics as "given" or "fixed." Each and every learner can experience mathematics through different practices and "own" mathematics as a human activity.
Problematizing what is important for students to learn in and through mathematics
The evolving conceptions about the nature of mathematics suggest that choices exist when deciding what and how to teach and learn mathematics but they do not specify what and how to make the choice. Decisions require articulating options for conceptions of what is important for students to learn in and through mathematics and evaluating the advantages and drawbacks for the students for each option.
According to Stanic and Kilpatrick (1992), the history of school mathematics curricula presents two important and real changes over the years: one is at the turn of the twentieth century when school mathematics was reformed as a unified and applied curriculum to accommodate dramatically increased student populations from diverse backgrounds, and the other is the "New Math" movement of the 1950s and 1960s, intended to integrate modern mathematics into school curriculum. The perceived failure of the "New Math" movement led to the "Back to Basics" movement in the 1970s, followed by "Problem Solving" in the 1980s, and then the Curriculum Standards movement in the 1990s and after. The history shows school mathematics curricula have emphasized teaching and learning mathematical knowledge and skills, together with problem solving and some applications of mathematics, a picture that is consistent with what Devlin (2000) refers to as the 1st face and some reference to the 4th face of mathematics.
Therefore, although there have been reforms in mathematics curriculum and instruction, there are hardly real changes in how mathematics is conceptualized and presented in school education in the USA (Stanic and Kilpatrick 1992) and other education systems (e.g., Leung and Li 2010; Li and Lappan 2014). The dominant conception remains mathematics as products, frequently referring to a body of static knowledge and skills that need to be learned and acquired (Fisher 1990). This continues to be largely the case in practice, despite advances in conceptualization (see below).
It should be noted that conceptualizing mathematics as "a body of knowledge and skills" is not wrong, especially with such a long history of knowledge creation and accumulation in mathematics, but it is not adequate for school mathematics nowadays. The set of concepts and procedures, after years of development, exceeds what could be covered in any school curricula. Moreover, this body of knowledge and skills keeps growing, as the product of human intelligence and scholarship in mathematics. Devlin (2012) pointed out that school mathematics mainly covers what was developed in the Greek mathematics, plus just two further advances from the seventh century: calculus and probability theory. It is no wonder if someone questions the value of learning such a small set of knowledge and skills developed more than a thousand years ago. Meanwhile, this body of knowledge and skills are often abstract, static, and "foreign" to many students and teachers who learned to perceive mathematics as an external entity in existence (Plato's notion) rather than Aristotelian emphasis on experimentation (Cooney 1987). It is thus not surprising for so many students and teachers to claim that mathematics is difficult (e.g., Fritz et al. 2019) and "it is ok—not everyone can be good at math" (Rattan et al. 2012).
What can be made meaningful should be critically important to those who want to (or need to) learn and teach mathematics. In fact, there is significant evidence that students often try to make sense of mathematics that is "presented" or "given" to them, although they made numerous errors that can be decoded to study their thinking (e.g., Ashlock 2010). Indeed, misconceptions are best thought of not as errors that need to be "fixed," but as plausible abstractions on the basis of what students have learned—i.e., attempts at sense-making (Smith et al. 1993). Conceiving mathematics as about "ideas," we can help students to play, own, experience, and think about some key ideas just like what they do in many other activities, such as game play (Gee 2005). Definitions of concepts and formal languages and procedures can be postponed until students are ready to consider why and how they are needed. Mathematics should be taken and accepted as a human activity (Dossey 1992), and developing students' mathematical thinking (about ideas) should be emphasized in learning mathematics itself (Devlin 2012) and in STEM (Li et al. 2019a).
Along with the shift from products to ideas in mathematics, scholars have already focused on how people work with ideas in mathematics. Elaborated in detail by Schoenfeld (in press), the revolution began with George Pólya (1887–1985) who had a fundamental interest in having students learn and understand content via problem solving. For Pólya, mathematics was about inquiry, sense making, and understanding how and why mathematical ideas (instead of content as products) fit together the way they do. The call for problem solving in the 1980s in the USA was (at least partially) inspired by Pólya's ideas after a decade of "back to basics" in the 1970s. It has been recognized since that the practices of mathematics (including problem solving) are every bit as important as the content itself, and the two shouldn't be separated. In the follow-up standards movement, the content and practices have been the "warp and weave" of the fabric doing mathematics, as articulated in Principles and Standards for School Standards (NCTM 2000). There were five content standards and five process standards (i.e., problem solving, reasoning, connecting, communicating, representing). It is widely acknowledged, also in the Common Core State Standards in the USA (CCSSI 2010), that both content and processes/practices are essential and they form the base for next steps.
Problematizing how mathematics is taught and learned, with connections to STEM education
How the ways that mathematics is often taught cause concerns
Conceiving mathematics as a body of facts and procedures to be "mastered" has been long-standing in mathematics education practice, and it often results in students' learning by rote memorization. For example, Schoenfeld (1988) provided a detailed account of the disasters of a "well-taught" mathematics course, documenting a 10th-grade geometry class taught by a confident and experienced teacher. The teacher taught and managed his class well, and his students also did well on standardized examinations, which focused on content and procedures. At the same time, however, Schoenfeld pointed out that the students developed counterproductive views of mathematics. Although the students developed some level of proficiency in content and procedures, they gained (or were reinforced in) the kinds of beliefs about mathematics as being fragmented and disconnected. Schoenfeld argued that the course led students to develop a robust and counterproductive set of beliefs about the nature of geometry.
Seeking possible origins about students' counterproductive beliefs about mathematics from mathematics instruction motivated Schoenfeld's study (Schoenfeld 1988). Such an intuitive motivation is also evident in other studies. Keitel (2006) compared the lessons of two teachers (T1 and T2) in Germany who taught their classes very differently. T1 regularly taught the class emphasizing routine individual practice and memorization of specific algebraic rules. T1 emphasized the importance of such practices for test taking, and the students followed his instruction. Even when T1 one day introduced a non-routine problem that connects algebra and geometry, the overwhelming emphasis on mastering routines and algorithms seemed to overshadow in dealing such a non-routine problem. In contrast, T2's teaching emphasized students' initiatives and collaboration, although T2 also used formal routine tasks. At the end, students in T2's class reported positively about their experience, enjoyed working together, and appreciated the opportunities of thinking mathematically. Studies by Schoenfeld (1988) and Keitel (2006) indicate how students' experience in mathematics classes influences their perceptions of mathematics and also imply the importance of learning about teachers' perceptions of mathematics that likely guide their instructional practice (Cooney 1987).
Rattan et al. (2012) found that teachers with different perceptions of mathematics teach differently. Specifically, Rattan et al. looked at these teachers holding an entity (fixed) theory of mathematics intelligence (G1) versus incremental theory (G2). Through their studies, Rattan and colleagues found that G1 teachers more readily judged students to have low ability, comforted students for low mathematical ability, and used "kind" strategies (e.g., assigning less homework) unlikely to promote their engagement with the field than G2 teachers. Students who received comfort-oriented feedback perceived their teachers' entity theory and low expectations and reported lowered motivation and expectations for their own performance. The results suggest how teachers' inadequate perceptions of mathematics and beliefs about the nature of students' mathematical intelligence contributed to low achievement, diminished self-esteem and viewed mathematics is only a set of static facts and procedures. Further, the results suggest that how mathematics is taught influences more than students' proficiency with mathematics content in a class. Sun (2018) made a similar argument after synthesizing existing literature and analyzing classroom observation data.
Based on the 2012 US national survey of science and mathematics education conducted by Horizon Research, Banilower et al. (2013) reported that a vast majority of mathematics teachers, from 81% at the high school level to 90% at the elementary level, believe that students should be given definitions of new vocabulary at the beginning of instruction on a mathematical idea. Also, many teachers believe that they should explain an idea to students before having them consider evidence for it and that hands-on activities should be used primarily to reinforce ideas students have already learned. The report suggests many teachers emphasized pedagogical practices of "give" and "present," perhaps influenced by conceptions of mathematics that are more Platonic than Aristotelian, similar to what was reported about teachers' practices more than two decades ago (Cooney 1987).
How to change?
Given that the evidence demonstrates a compelling case for changing how mathematics is taught, we turn our attention to suggesting how to realize this transformation. Changing how mathematics is taught and learned is not a new endeavor for both mathematics educators and mathematicians (e.g., Li, Silver, and Li 2014; Schoenfeld in press). For example, the "Moore Method," developed and used by Robert Lee Moore (a famous topologist) in the early twentieth century, shifted instruction from teacher-centered lecturing to student-centered mathematical development (Coppin et al. 2009). In its purest form, students were presented with mathematical definitions and asked to develop and/or prove theorems from them after class, without reading mathematics books or using other resources. When students returned to the class, they were asked to prove a theorem. As a result, students developed the mathematics themselves, instead of the instructor presenting the proofs and doing the mathematics for students. The method has had its own success in producing many great mathematicians; however, the high-pressure environment also drowned many students who might have been successful otherwise (Schoenfeld in press).
Although the "Moore Method" was used primarily in advanced mathematics courses at the post-secondary level, it illustrates how a different conception of mathematics led to a different instructional approach in which students developed mathematics. However, it might be the opposite end of a spectrum, in comparison to approaches that present mathematics to students in accommodating and easy-to-digest ways that can be as much easy as possible. Neither extreme is a good option for K-12 students. Again, it becomes important for us to consider options that can support the value of learning mathematics.
Our discussion in the previous section highlights the importance of taking mathematics as a human activity, ensuring it is meaningful to students, and developing students' mathematical thinking about ideas, rather than simply absorbing a set of static and disconnected knowledge and skills. We call for a shift in teaching mathematics based on Platonic conceptions to approaches based on more of Aristotelian conceptions. In essence, Plato emphasized ideal forms of mathematical objects, perhaps inaccessible through people's sense making efforts. As a result, learners lack ownership of the ideal forms of mathematical objects, because mathematical objects cannot and should not be created by human reasoning. In contrast, Aristotle emphasized that mathematical objects are developed through logic reasoning and empirical realization. In other words, mathematical objects exist only when they can be sensed and verified by people's efforts. This differs from Plato's passive perspective, highlights human ownership of mathematical ideas and encourages people to make mathematics make sense, termed as making sense by McCallum (2018). Aristotelian conceptions view mathematics as objects that learners can actively develop and structure as mathematically meaningful, which is more in line with what research mathematicians do. McCallum (2018) argued that both sense-making and making-sense stances are needed for a complete view of mathematics and learning, recognizing that not attending to both stances carries risks. "Just as it is a risk of the sense-making stance that the mathematics gets ignored, it is a risk of the making-sense stance that the sense-maker gets ignored." (McCallum 2018).
In addition, there is the issue of personal identity: if students come to avoid mathematics because they are uncomfortable with it (in fact, mathematics anxiety has become a widespread problem for all ages across the globe, see Luttenberger et al. 2018) then mathematics instruction has failed them, regardless of test scores.
In the following, we discuss sense-making and making-sense stances first with specific examples from mathematics. Then, we discuss connections to STEM education.
Sense making is much more than the acquisition of knowledge and skills
Sense making has long been emphasized in mathematics education community. William A. Brownell is a well-known, early 20th century scholar who advocated the value of sense making in the learning of mathematics. For example, Brownell (1945) discussed how arithmetic can and should be taught and learned not only as procedures, but also as a meaningful system of thinking. He shared many examples like the following division,
$$ 8\overline{\Big)576\ } $$
Brownell suggested to ask questions: what does the 5 of 576 mean? Why must 57 be the first partial dividend? Do you actually divide 8 into 57, or into 57…'s? etc., instead of simply letting students memorize how to carry out the procedure. What Brownell advocated has been commonly accepted and emphasized in mathematics education nowadays as sense making (e.g., Schoenfeld 1992).
There can be different ways of sense making of the same computation. As an example, the sense making process for the above long division can come out with mental math as: I am looking to see how close I can get to 570 with multiples of 80; 7 multiples of 80 gives me 560, which is close. Of course, given base 10 notation, that's the same as 8 multiples of 70, which is why the 7 goes over the 57. And when I subtract 560, there are 16 left over, so that's another 2 8 s. Such a sense-making process also works, as finding the answer (quotient, k) of 576 ÷ 8 is the same operation as to find k that satisfies 576 = k × 8. In mathematics, division and multiplication are alternate but equivalent ways of doing the same operation.
To help students build numerical reasoning and make sense of computations, many teachers use number talks in their classrooms for students to practice and share these mental math and computation strategies (e.g., Parrish 2011). In fact, new terms are being created and used in mathematics education about sense making, such as number sense (e.g., Sowder 1992) and symbol sense (Arcavi, 1994). Some instructional programs, such as Cognitively Guided Instruction (see, e.g., Carpenter et al., 1997, 1998), make sense making the core of instructional activities. We argue that such activities should be more widely adopted.
Making sense makes the other side of mathematical practice visible, and values idea development and ownership
The making-sense stance, as termed by McCallum (2018), is not commonly practiced as it is pertinent to expert mathematician's practices. Where sense making (as discussed previously) emphasizes the process of making sense of what is being learned, making sense emphasizes the process of making mathematics make sense. Making sense highlights the importance for students to experience mathematics through creating, designing, developing, and connecting mathematical ideas. As an example, for the above division computation, 8\( \overline{\Big)576\ } \), students may wonder why the division procedure is performed from left to right, which is different from the other operations (addition, subtraction, and multiplication) that are all performed from right to left. In fact, students can be encouraged to explore if the division can also be performed from right to left (i.e., starting from the one's place). They may discover, with possible support from the teacher, that the division can be done in this way. However, once the division is moved to the high-value places, it will require the process to go back down to the low-value places for completion. In other words, the division process starting from the low-value place would require repeated processes of returning to the low-value places; as a result, it is inefficient. As mathematical procedure is designed to improve efficiency, the division procedure is thus set to be carried out from the high-value place to low-value place (i.e., from left to right). Students who work this out experience mathematics more deeply than the sense-making described by Brownell (1945).
There are plenty of making-sense opportunities in classroom instruction. For example, kindergarten children are often given opportunities to play with manipulatives like cube trains and snub cubes, to explore and learn about patterns, numbers, and measurement through various connections. The recording of such activities typically results in numerical expressions or operations of these connections. In addition, such activities can also serve as a context to encourage students to design and create a way of "recording" these connections directly with a drawing line next to the connected train cubes. Such a design activity will help students to develop the concept of a number line that includes the original/starting point, unit, and direction (i.e., making mathematics make sense), instead of introducing the number line to students as a mathematical concept being "given" years later.
Learning how to provide students with opportunities to develop mathematics may occur with experience. Huang et al. (2010) found that expert and novice teachers in China both valued students' mastering of mathematical knowledge and skills and their development in mathematical thinking methods and abilities. However, novice teachers were particularly concerned about the effectiveness of their guidance, in contrast to expert teachers who emphasized the development of students' mathematical thinking and higher-order thinking abilities and properly dealing with important and difficult content points. The results suggest that teachers' perceptions and pedagogical practices can change and improve over time. However, it may be worth asking if support for teacher development would accelerate the process.
Connecting changes in mathematics and STEM education
Although it is commonly acknowledged that mathematics is foundational to STEM, mathematics is being related to STEM education at a distance in practice and also in scholarship development (English 2016, see additional notes at the end of this editorial). Holding the conception of mathematics as products does not support integrating mathematics with other STEM disciplines, as mathematics can be perceived simply as a set of tools for these disciplines. At the same time, mathematics and science have often proceeded along parallel tracks, with mathematics focused on "problem solving" while science has focused on "inquiry." To better connect mathematics and other disciplines in STEM, we should focus on ideas and thinking development in mathematics (Li et al. 2019a), unifying instruction from the student perspective (the Teaching for Robust Understanding framework, discussed below).
Emphasizing both sense making and making sense in mathematics education opens opportunities for connections with similar practices in other STEM disciplines. For example, sense making is very much emphasized in science education (Hogan 2019; Kapon 2017; Odden and Russ 2019), often combined with reflections in engineering (Kilgore et al. 2013; Turns et al. 2014), and also in the context of using technology (e.g., Antonietti and Cantoia 2000; Dick and Hollebrands 2011). Science is fundamentally about discovery and understanding of the natural world. This notion provides a natural link to mathematical modeling (e.g., Burkhardt 1981). Beyond that, in science education, sense making places a heavy focus on the construction and evaluation of explanation (Kapon 2017), and can even be defined as a process of constructing an explanation to resolve a perceived gap or conflict in knowledge (Odden and Russ 2019). Design and making play vital roles in engineering and technology education (Dym et al., 2005), as is student reflection on these experiences (e.g., Turns et al. 2014). Indeed, STEM disciplines share the same conceptual process of sense making as learners, individually or in a group, actively engage with the natural or man-made world, explore it, and then develop, test, refine, and use ideas together with specific explanation. If mathematics was conceived as an "empirical" discipline, connections with other STEM disciplines would be strengthened. In philosophical terms, Lakatos (1976) made similar claims Footnote 1.
Similar to the emphasis on sense making placed in the Mathematics Curriculum Standards (e.g., NCTM, 1989, 2000), Next Generation Science Standards (NGSS Lead States 2013) prompted a shift in science education away from simply knowing science content and procedures to practicing and using science, together with engineering, to make sense of the world and create the future. In a review, Fitzgerald and Palincsar (2019) concluded sense making is a productive lens for investigating and characterizing great teaching across multiple disciplines.
Mathematics has stronger linkages to creation and design than traditionally imagined. Therefore, its connections to engineering and technology could be much stronger. However, the deep-rooted conception of mathematics as products has traditionally discouraged students and teachers from considering and valuing design and design thinking (Li et al. 2019b). Conceiving mathematics as making sense should help promote conceptual changes in mathematical practice to value idea generation and design activity. Connections generated from such a shift will support teaching and learning not only in individual STEM disciplines, but also in integrated STEM education.
At the same time, although STEM education as a commonly recognized field does not have a long history (Li 2014, 2018a), its rapid development can help introduce ideas for exploring how mathematics can be taught and learned. For example, the concept of projects is common in engineering professional practice, and the project-based learning (PjBL) as an instructional approach is a key component in some engineering programs (e.g., Berger 2016; de los Ríos et al. 2010; Mills and Treagust 2003). de los Ríos et al. (2010) highlighted three main advantages of PjBL: (1) development in technical, personal, and contextual competences; (2) students' engagement with real problems from professional contexts; and (3) collaborative learning facilitated through the integration of teaching and research. Such advantages are important for students' learning of mathematics and are aligned well with efforts to develop 21st century skills, including problem solving, communication, collaboration, and critical thinking.
Design-based learning (DBL) is another instructional approach commonly used in engineering and technology fields. Gómez Puente et al. (2013) conducted a sampled review and concluded that DBL projects consist of open-ended, hands-on, authentic, and multidisciplinary design tasks. Teachers using DBL facilitate both the process for students to gain domain-specific knowledge and thinking activities to generate innovative solutions. Such features could be adapted for mathematics education, especially integrated STEM education, in concert with design and design thinking. In addition to a few examples discussed above about making sense in mathematics, there is a growing body of publications developed by and for mathematics teachers with specific examples of investigations, design projects, and instructional activities associated with STEM (Li et al. 2019b).
A framework for helping students to gain important experiences in and through mathematics, as connected to other disciplines in STEM
For observing and evaluating classroom instruction in general and mathematics classroom instruction in specific, there are several widely used frameworks and rubrics available. However, a trial use of selected frameworks with sampled mathematics classroom instruction episodes suggested their disagreements on what counts as high-quality instruction, especially with aspects on disciplinary thinking being valued and relevant classroom practices (Schoenfeld et al. 2018). The results suggest the importance of choice making, when we consider a framework in discussing and evaluating teaching practices.
Our discussion above highlights the importance of shifting away from viewing mathematics simply as a set of static knowledge and skills, to focusing on ideas and thinking development in teaching and learning mathematics. Further discussion of several aspects of changes specifies the needs of developing and using practices associated with sense making, making sense, and connecting mathematics and STEM education for changes.
To support effective mathematics instruction, we propose the use of the Teaching for Robust Understanding (TRU) framework to help characterize powerful learning environments. With the conception of mathematics as "empirical" and a focus on students' experience, then the focus of instruction should also be changed. We argue that shift is from instruction conceived as "what should the teacher do" to instruction conceived as "what mathematical experiences should students have in order for them to develop into powerful thinkers?" It is the shift in the frame of TRU that makes it so powerful and pertinent for all these proposed changes. Moreover, TRU only uses a small number of actionable dimensions after distilling the literature on teaching for robust or powerful understanding. That makes TRU a practical mechanism for problematizing instruction.
Figure 1 presents the TRU Math framework that identifies five key dimensions along which powerful classroom environments can be characterized: the mathematics; cognitive demand; equitable access; agency, ownership, and identity; and formative assessment. These five dimensions were distilled from an extensive literature review, thus capturing what the literature considers to be essential. They were tested against classroom videotapes and data on student performance, and the results indicated that classrooms that did well on the TRU dimensions produced students who did correspondingly well on tests of mathematical knowledge, thinking, and problem solving (e.g., Schoenfeld 2014, 2019). In brief, the argument regarding the importance of the five dimensions of TRU Math is as follows. First, the quality of the mathematics discussed (dimension 1) is critical. What individual students learn is unlikely to be richer than what they experience in the classroom. Whether individual students' understanding rises to the level of what is discussed/presented in the classroom depends on other factors, which are captured in the remaining four dimensions. For example, you surely have had the experience, at a lecture, of hearing beautiful content presented, and then not being able to do any of the assigned problems! The remaining four dimensions capture aspects needed to support the development of all students with respect to sense making, making sense, ownership, and feedback loop. Dimension 2: Cognitive Demand. Are students engaged in sense making and making sense? Are they engaged in "productive struggle"? Dimension 3: Equitable Access. Are all students fully engaged with the central content and practices of the domain so that every student can profit from it? Dimension 4: Agency, Ownership, and Identity. Do all students have opportunities to develop idea ownership and mathematical agency? Dimension 5: Formative Assessment. Are students encouraged and supported to share their thinking with a meaningful feedback loop for instructional adjustment and improvement?

The TRU Mathematics Framework: The five dimensions of powerful mathematics classrooms
Full size image
The first key point about TRU is that students learn more in classrooms that are powerful along the five TRU dimensions. Second, the shift of attention from the teacher to the environment is fundamentally important. The key question is not "Is the teacher doing particular things to support learning?"; instead, it is, "Are students experiencing instruction so that it is conducive to their growth as mathematical thinkers and learners?" Third, the framework is not prescriptive; it respects teacher autonomy. There are many ways to be an excellent teacher. The question is, Does the learning environment created by the teacher provide each student rich opportunities along the five dimensions of the framework? Specifically, in describing the dimensions of powerful instruction, the framework serves to problematize instruction. Asking "how am I doing along each dimension; how can I improve?" can lead to richer instruction without prescribing or imposing a particular style or particular norms on teachers.
Extending to STEM education
Now, we suggest the following. If you teach biology, chemistry, physics, engineering, or any other STEM field, replace "mathematics" in Fig. 1 with your discipline. The first dimension is about rich content and practices in your field. And the remaining four dimensions are about necessary aspects of your students' classroom engagement with the discipline. Practices associated with sense making, making sense, and STEM education are all be reflected in these five dimensions, with central attention on students' experience in such classroom environments. Although the TRU framework was originally developed for characterizing effective mathematics classroom environments, it has been carefully framed in a way that is applicable to many different disciplines (Schoenfeld 2014). Our discussion above already specified why sense making, making sense, and specific instructional approaches like PjBL and DBL are shared across disciplines in STEM education. Thus, the TRU framework is applicable to other STEM disciplines. The natural analogue of the TRU framework for any field is given in Fig. 2.
The domain-general version of the TRU framework
Full size image
Both the San Francisco Unified School District and the Chicago Public Schools adopted the TRU Math framework and found results within mathematics sufficiently promising that they expanded their efforts to all subject areas for professional development and instruction, using the domain-general TRU framework. Work is still in its early stages. Current efforts might be best conceptualized as a laboratory for exploration rather than a promissory note for improvement across all different disciplines. It will take time to accumulate data to show effectiveness. For further information about the domain-general TRU framework and tools for professional development are available at the TRU framework website, https://truframework.org/
Finally, as a framework, TRU is not a set of specific tools or guidelines, although it can be used to guide their development. To help lead our discussion to something more practical, we can use the framework to check and identify aspects that are typically under-emphasized and move them to center stage in order to improve classroom instruction. Specifically, the following is a list of sample under-emphasized norms and practices that can be identified (Schoenfeld in press).
- (1)
Establishing a climate of inquiry, in which mathematics is experienced as a discipline of exploration and sense making.
- (2)
Developing students' ownership of ideas through the process of developing, sharing, refining, and using ideas; concepts and language can come later.
- (3)
Focusing on big ideas, and not losing the forest for the trees.
- (4)
Making student thinking central to classroom discourse.
- (5)
Ensuring that classroom discourse is respectful and inviting.
Where to start? Begin by problematizing teaching and the nature of learning environments
Here we start by stipulating that STEM disciplines as practiced, are living, breathing fields of inquiry. Knowledge is important; ideas are important; practices are important. The list given above applied to all STEM disciplines, not just mathematics.
The issue, then, is developing teacher capacity to craft environments that have the properties described immediately above. Here we share some thoughts, and the topic itself can well be discussed extensively in another paper. To make changes in teaching, it should start with assessing and changing teaching practice itself (Hiebert and Morris 2012). Opening up teachers' perceptions of teaching practices should not be done by telling teachers what to do!—the same rules of learning apply to teachers as they apply to students. Learning environments for teachers should offer teachers the same opportunities for rich engagement, challenge, equitable access, and ownership as we hope students will experience (Schoenfeld 2015). Working together with teachers to study and reflect on their teaching practices in light of the TRU framework, we can help teachers to find out what their students are experiencing and why changes are needed. The framework can also help guide teachers to learn what changes would be needed, and to try out changes to learn how their students' learning may differ. It is this iterative and concrete process that can hopefully help shift participating teachers' perceptions of mathematics. Many tools for problematizing teaching are available at the TRU web site (see https://truframework.org/). If teachers can work together with a focus on selected lessons like what teachers often do in China, the process would help form a school-based learning community that can contribute to not only participating teachers' practice change but also their expertise improvement (Huang et al. 2011; Li and Huang 2013).
Notes
As reported before (Li 2018b), publications in the International Journal of STEM Education show a mix of individual-disciplinary and multidisciplinary education in STEM over the past several years. Although one journal's publications are limited in its scope of providing a picture about the scholarship development related to mathematics and STEM education, it can allow us to get a sense of related development.
If taking a closer look at the journal's publications over the past three years from 2016 to 2018, we found that the number of articles published with a clear focus on mathematics is relatively small: three (out of 21) in 2016, six (out of 34) in 2017, and five (out of 56) in 2018. At the same time, we should point out that these publications from 2016 to 2018 seem to reflect a trend, over these three years, of moving toward issues that can go beyond mathematics itself, as what was noted before (Li 2018b). Specifically, for these three articles published in 2016, they are all about mathematics education at either elementary school (Ding 2016; Zhao et al. 2016) or university levels (Schoenfeld et al. 2016). Out of the six published in 2017, three are on mathematics education (Hagman et al. 2017; Keller et al. 2017; Ulrich and Wilkins 2017) and the other three on either teacher professional development (Borko et al. 2017; Jacobs et al. 2017) or connection with engineering (Jehopio and Wesonga 2017). For the five published in 2018, two are on mathematics education (Beumann and Wegner 2018; Wilkins and Norton 2018) and the other three have close association with other disciplines in STEM (Blotnicky et al. 2018; Hayward and Laursen 2018; Nye et al. 2018). This trend likely reflects a growing interest, with close connection to mathematics, in both mathematics education community and a broader STEM education community of developing and sharing multidisciplinary and interdisciplinary scholarship.
Availability of data and materials
Not applicable
Notes
- 1.
Interestingly, Lakatos was advised by both Popper and Pólya—his ideas being in some ways a unification of Pólya's emphasis on mathematics as an empirical discipline and Popper's reflections on the nature of the scientific endeavor.
References
-
Antonietti, A., & Cantoia, M. (2000). To see a painting versus to walk in a painting: An experiment on sense-making through virtual reality. Computers & Education, 34, 213–223.
Article Google Scholar
-
Arcavi, A. (1994). Symbol sense: Informal sense-making in formal mathematics. For the Learning of Mathematics, 14(3), 24–35.
Google Scholar
-
Ashlock, R. B. (2010). Error patterns in computation (Tenth Edition). Boston, MA: Allyn & Bacon.
Google Scholar
-
Banilower, E. R., Smith, P. S., Weiss, I. R., Malzahn, K. A., Campbell, K. M., et al. (2013). Report of the 2012 national survey of science and mathematics education. Horizon Research, Chapel Hill, NC. Retrieved from http://www.nnstoy.org/download/stem/2012%20NSSME%20Full%20Report.pdf
-
Berger, C. (2016). Engineering is perfect for K-5 project-based learning. Engineering is Elementary (EiE) Blog, https://blog.eie.org/engineering-is-perfect-for-k-5-project-based-learning
-
Beumann, S. & Wegner, S.-A. (2018). An outlook on self-assessment of homework assignments in higher mathematics education. International Journal of STEM Education, 5:55. https://doi.org/10.1186/s40594-018-0146-z
-
Blotnicky, K. A., Franz-Odendaal, T., French, F., & Joy, P. (2018). A study of the correlation between STEM career knowledge, mathematics self-efficacy, career interests, and career activities on the likelihood of pursuing a STEM career among middle school students. International Journal of STEM Education, 5:22. https://doi.org/10.1186/s40594-018-0118-3
-
Borko, H., Carlson, J., Mangram, C., Anderson, R., Fong, A., Million, S., Mozenter, S., & Villa, A. M. (2017). The role of video-based discussion in model for preparing professional development leaders. International Journal of STEM Education, 4:29. https://doi.org/10.1186/s40594-017-0090-3
-
Boyer, C. B. (1991). A history of mathematics (2nd ed.). New York: Wiley.
Google Scholar
-
Brownell, W. A. (1945). When is arithmetic meaningful? The Journal of Educational Research, 38(7), 481–498.
Article Google Scholar
-
Burkhardt, H. (1981). The real world and mathematics. Glasgow: Blackie, reissued Nottingham: Shell Centre Publications.
-
Carpenter, T., Fennema, E., & Franke, M. (1997). Cognitively guided instruction: A knowledge base for reform in primary mathematics instruction. Elementary School Journal, 97, 3–20.
-
Carpenter, T., Franke, M., Jacobs, V. R., & Fennema, E. (1998). A longitudinal study of invention and understanding in children's multidigit addition and subtraction. Journal for Research in Mathematics Education, 29(1), 3–20.
Article Google Scholar
-
Committee on STEM Education, National Science & Technology Council, the White House (2018). Charting a course for success: America's strategy for STEM education. Washington, DC. https://www.whitehouse.gov/wp-content/uploads/2018/12/STEM-Education-Strategic-Plan-2018.pdf Retrieved on 18 January, 2019.
-
Common Core State Standards Initiative (CCSSI). (2010). Common core state standards for mathematics. Retrieved from http://www.corestandards.org/Math/Practice
-
Cooney, T (1987). The issue of reform: What have we learned from yesteryear? In Mathematical Sciences Education Board, The teacher of mathematics: Issues for today and tomorrow (pp. 17-35). Washington, DC: National Academy Press.
-
Coppin, C. A., Mahavier, W. T., May, E. L., & Parker, E. (2009). The Moore Method. Washington, DC: Mathematical Association of America.
Google Scholar
-
Davis, P., & Hersh, R. (1980). The mathematical experience. Boston: Birkhauser.
Google Scholar
-
de los Ríos, I., Cazorla, A., Díaz-Puente, J. M., & Yagüe, J. L. (2010). Project–based learning in engineering higher education: Two decades of teaching competences in real environments. Procedia Social and Behavioral Sciences, 2, 1368–1378.
Article Google Scholar
-
Devlin, K. (2000). The four faces of mathematics. In M. J. Burke & F. R. Curcio (Eds.), Learning Mathematics for a New Century: 2000 Yearbook of the National Council of Teachers of Mathematics (pp. 16–27). Reston, VA: NCTM.
Google Scholar
-
Devlin, K. (2012). Introduction to mathematical thinking. Stanford, CA: The author.
-
Dick, T. P., & Hollebrands, K. F. (2011). Focus on high school mathematics: Technology to support reasoning and sense making. Reston, VA: NCTM.
Google Scholar
-
Ding, M. (2016). Developing preservice elementary teachers' specialized content knowledge: The case of associative property. International Journal of STEM Education, 3, 9 https://doi.org/10.1186/s40594-016-0041-4.
Article Google Scholar
-
Dossey, J. A. (1992). The nature of mathematics: Its role and its influence. In D. Grouws (Ed.), Handbook for Research on Mathematics Teaching and Learning (pp. 39–48). New York: MacMillan.
Google Scholar
-
Dossey, J. A., McCrone, S. S., & Halvorsen, K. T. (2016). Mathematics education in the United States 2016: A capsule summary fact book. Reston, VA: The National Council of Teachers of Mathematics.
Google Scholar
-
Dym, C. L., Agogino, A. M., Eris, O., Frey, D. D., & Leifer, L. J. (2005). Engineering design thinking, teaching, and learning. Journal of Engineering Education, 94(1), 103–120.
Article Google Scholar
-
English, L. D. (2016). STEM education K-12: Perspectives on integration. International Journal of STEM Education, 3:3, https://doi.org/10.1186/s40594-016-0036-1
-
Fisher, C. (1990). The research agenda project as prologue. Journal for Research in Mathematics Education, 21, 81–89.
Article Google Scholar
-
Fitzgerald, M. S., & Palincsar, A. S. (2019). Teaching practices that support student sensemaking across grades and disciplines: A conceptual review. Review of Research in Education, 43, 227–248.
Article Google Scholar
-
Fritz, A., Haase, V. G., & Rasanen, P. (Eds.). (2019). International handbook of mathematical learning difficulties. Cham, Switzerland: Springer.
Google Scholar
-
Gee, J. P. (2005). What would a state of the art instructional video game look like? Innovate: Journal of Online Education, 1(6) Retrieved from https://nsuworks.nova.edu/innovate/vol1/iss6/1.
-
Gómez Puente, S. M., van Eijck, M., & Jochems, W. (2013). A sampled literature review of design-based learning approaches: A search for key characteristics. International Journal of Technology and Design Education. https://doi.org/10.1007/s10798-012-9212-x.
Article Google Scholar
-
Hagman, J. E., Johnson, E., & Fosdick, B. K. (2017). Factors contributing to students and instructors experiencing a lack of time in college calculus. International Journal of STEM Education, 4, 12 https://doi.org/10.1186/s40594-017-0070-7.
Article Google Scholar
-
Hayward, C. N. & Laursen, S. L. (2018). Supporting instructional change in mathematics: Using social network analysis to understand online support processes following professional development workshops. International Journal of STEM Education, 5:28. https://doi.org/10.1186/s40594-018-0120-9
-
Hersh, R. (1986). Some proposals for reviving the philosophy of mathematics. In T. Tymoczko (Ed.), New directions in the philosophy of mathematics (pp. 9–28). Boston: Birkhauser.
Google Scholar
-
Hiebert, J., & Morris, A. K. (2012). Teaching, rather than teachers, as a path toward improving classroom instruction. Journal of Teacher Education, 63(2), 92–102.
Article Google Scholar
-
Hogan, M. (2019). Sense-making is the core of NGSS. In Illuminate education blog, https://www.illuminateed.com/blog/2019/03/sense-making-is-the-core-of-ngss/ Accessed 15 Oct 2019.
-
Huang, R., Li, Y., & He, X. (2010). What constitutes effective mathematics instruction: A comparison of Chinese expert and novice teachers' views. Canadian Journal of Science, Mathematics and Technology Education, 10(4), 293-306. https://doi.org/10.1080/14926156.2010.524965
Article Google Scholar
-
Huang, R., Li, Y., Zhang, J., & Li, X. (2011). Improving teachers' expertise in mathematics instruction through exemplary lesson development. ZDM – The International Journal on Mathematics Education, 43(6-7), 805–817.
Article Google Scholar
-
Jacobs, J., Seago, N., & Koellner, K. (2017). Preparing facilitators to use and adapt mathematics professional development materials productively. International Journal of STEM Education, 4, 30 https://doi.org/10.1186/s40594-017-0089-9.
Article Google Scholar
-
Jehopio, P. J., & Wesonga, R. (2017). Polytechnic engineering mathematics: assessing its relevance to the productivity of industries in Uganda. International Journal of STEM Education, 4, 16 https://doi.org/10.1186/s40594-017-0078-z.
Article Google Scholar
-
Kapon, S. (2017). Unpacking sensemaking. Science Education, 101(1), 165–198.
Article Google Scholar
-
Keitel, C. (2006). 'Setting a task' in German schools: Different frames for different ambitions. In D. Clarke, C. Keitel, & Y. Shimizu (Eds.), Mathematics classrooms in 12 countries: The insiders' perspective (pp. 37–58). Rotterdam Netherlands: Sense Publishers.
Google Scholar
-
Keller, R. E., Johnson, E., & DeShong, S. (2017). A structural equation model looking at student's participatory behavior and their success in Calculus I. International Journal of STEM Education, 4, 24 https://doi.org/10.1186/s40594-017-0093-0.
Article Google Scholar
-
Kilgore, D., Sattler, B., & Turns, J. (2013). From fragmentation to continuity: Engineering students making sense of experience through the development of a professional portfolio. Studies in Higher Education, 38(6), 807–826.
Article Google Scholar
-
Kline, M. (1973). Why Johnny can't add: The failure of new math. New York: St. Martin's.
Google Scholar
-
Lakatos, I. (1976). Proofs and refutations: The logic of mathematical discovery. Cambridge, England: Cambridge University Press.
Book Google Scholar
-
Leung, F. K. S., & Li, Y. (Eds.). (2010). Reforms and issues in school mathematics in East Asia – Sharing and understanding mathematics education policies and practices. Rotterdam, Netherlands: Sense Publishers.
Google Scholar
-
Li, Y. (2014). International Journal of STEM Education – A platform to promote STEM education and research worldwide. International Journal of STEM Education, 1, 1 https://doi.org/10.1186/2196-7822-1-1.
Article Google Scholar
-
Li, Y. (2018a). Journal for STEM Education Research – Promoting the development of interdisciplinary research in STEM education. Journal for STEM Education Research, 1(1-2), 1–6 https://doi.org/10.1007/s41979-018-0009-z.
Article Google Scholar
-
Li, Y. (2018b). Four years of development as a gathering place for international researcher and readers in STEM education. International Journal of STEM Education, 5, 54 https://doi.org/10.1186/s40594-018-0153-0.
Article Google Scholar
-
Li, Y., & Huang, R. (Eds.). (2013). How Chinese teach mathematics and improve teaching. New York: Routledge.
Google Scholar
-
Li, Y., & Lappan, G. (Eds.). (2014). Mathematics curriculum in school education. Dordrecht: Springer.
Google Scholar
-
Li, Y., Schoenfeld, A. H., diSessa, A. A., Grasser, A. C., Benson, L. C., English, L. D., & Duschl, R. A. (2019a). On thinking and STEM education. Journal for STEM Education Research, 2(1), 1–13. https://doi.org/10.1007/s41979-019-00014-x.
Article Google Scholar
-
Li, Y., Schoenfeld, A. H., diSessa, A. A., Grasser, A. C., Benson, L. C., English, L. D., & Duschl, R. A. (2019b). Design and design thinking in STEM education. Journal for STEM Education Research, 2(2), 93-104. https://doi.org/10.1007/s41979-019-00020-z.
Article Google Scholar
-
Li, Y., Silver, E. A., & Li, S. (Eds.). (2014). Transforming mathematics instruction: Multiple approaches and practices. Cham, Switzerland: Springer.
Google Scholar
-
Luttenberger, S., Wimmer, S., & Paechter, M. (2018). Spotlight on math anxiety. Psychology Research and Behavior Management, 11, 311–322.
Article Google Scholar
-
McCallum, W. (2018). Sense-making and making sense. https://blogs.ams.org/matheducation/2018/12/05/sense-making-and-making-sense/ Retrieved on October 1, 2019.
-
Mills, J. E. & Treagust, D. F. (2003). Engineering education – Is problem-based or project-based learning the answer? Australasian Journal of Engineering Education, https://www.researchgate.net/profile/Nathan_Scott2/publication/238670687_AUSTRALASIAN_JOURNAL_OF_ENGINEERING_EDUCATION_Co-Editors/links/0deec53a08c7553c37000000.pdf Retrieved on October 15, 2019.
-
National Council of Teachers of Mathematics (NCTM). (1989). Curriculum and evaluation standards for school mathematics. Reston, VA: NCTM.
Google Scholar
-
National Council of Teachers of Mathematics (NCTM). (2000). Principles and standards for school mathematics. Reston, VA: NCTM.
Google Scholar
-
NGSS Lead States. (2013). Next generation science standards: For states, by states. Washington, DC: National Academies Press.
Google Scholar
-
Nye, B., Pavlik Jr., P. I., Windsor, A., Olney, A. M., Hajeer, M., & Hu, X. (2018). SKOPE-IT (Shareable Knowledge Objects as Portable Intelligent Tutors): Overlaying natural language tutoring on an adaptive learning system for mathematics. International Journal of STEM Education, 5, 12 https://doi.org/10.1186/s40594-018-0109-4.
Article Google Scholar
-
Odden, T. O. B., & Russ, R. S. (2019). Defining sensemaking: Bringing clarity to a fragmented theoretical construct. Science Education, 103, 187–205.
Article Google Scholar
-
Parrish, S. D. (2011). Number talks build numberical reasoning. Teaching Children Mathematics, 18(3), 198–206.
Article Google Scholar
-
Rattan, A., Good, C., & Dweck, C. S. (2012). "It's ok – Not everyone can be good at math": Instructors with an entity theory comfort (and demotivate) students. Journal of Experimental Social Psychology. https://doi.org/10.1016/j.jesp.2011.12.012.
Article Google Scholar
-
Schoenfeld, A. H. (1988). When good teaching leads to bad results: The disasters of "well-taught" mathematics courses. Educational Psychologist, 23(2), 145–166.
Article Google Scholar
-
Schoenfeld, A. H. (1992). Learning to think mathematically: Problem solving, metacognition, and sense-making in mathematics. In D. Grouws (Ed.), Handbook for Research on Mathematics Teaching and Learning (pp. 334–370). New York: MacMillan.
Google Scholar
-
Schoenfeld, A. H. (2001). Mathematics education in the 20th century. In L. Corno (Ed.), Education across a century: The centennial volume (100th Yearbook of the National Society for the Study of Education) (pp. 239–278). Chicago, IL: National Society for the Study of Education.
Google Scholar
-
Schoenfeld, A. H. (2014). What makes for powerful classrooms, and how can we support teachers in creating them? A story of research and practice, productively interwined. Educational Researcher, 43(8), 404–412. https://doi.org/10.3102/0013189X1455.
Article Google Scholar
-
Schoenfeld, A. H. (2015). Thoughts on scale. ZDM, the International Journal of Mathematics Education, 47, 161–169. https://doi.org/10.1007/s11858-014-0662-3.
Article Google Scholar
-
Schoenfeld, A. H. (2019). Reframing teacher knowledge: A research and development agenda. ZDM – The International Journal on Mathematics Education. https://doi.org/10.1007/s11858-019-01057-5
-
Schoenfeld, A. H. (in press). Mathematical practices, in theory and practice. ZDM – The International Journal on Mathematics Education.
-
Schoenfeld, A. H., Floden, R., El Chidiac, F., Gillingham, D., Fink, H., Hu, S., Sayavedra, A., Weltman, A., & Zarkh, A. (2018). On classroom observations. Journal for STEM Educ Res, 1(1-2), 34–59 https://doi.org/10.1007/s41979-018-0001-7.
Article Google Scholar
-
Schoenfeld, A. H., Thomas, M., & Barton, B. (2016). On understanding and improving the teaching of university mathematics. International Journal of STEM Education, 3, 4 https://doi.org/10.1186/s40594-016-0038-z.
Article Google Scholar
-
Smith, J., diSessa, A., & Roschelle, J. (1993). Misconceptions reconceived: A constructivist analysis of knowledge in transition. Journal of the Learning Sciences, 3(2), 115–163.
Article Google Scholar
-
Sowder, J. (1992). Estimation and number sense. In D. Grouws (Ed.), Handbook for research on mathematics teaching and learning (pp. 371–389). New York: MacMillan.
Google Scholar
-
Stanic, G. M. A., & Kilpatrick, J. (1992). Mathematics curriculum reform in the United States: A historical perspective. International Journal of Educational Research, 17(5), 407–417.
Article Google Scholar
-
Sun, K. L. (2018). The role of mathematics teaching in fostering student growth mindset. Journal for Research in Mathematics Education, 49(3), 330–355.
Article Google Scholar
-
Turns, J. A., Sattler, B., Yasuhara, K., Borgford-Parnell, J. L., & Atman, C. J. (2014). Integrating reflection into engineering education. Proceedings of 2014 American Society of Engineering Education Annual Conference, Paper ID #9230.
-
Tymoczko, T. (1986). New directions in the philosophy of mathematics. Boston: Birkhauser.
Google Scholar
-
Ulrich, C., & Wilkins, J. L. M. (2017). Using written work to investigate stages in sixth-grade students' construction and coordination of units. International Journal of STEM Education, 4, 23 https://doi.org/10.1186/s40594-017-0085-0.
Article Google Scholar
-
Wilkins, J. L. M., & Norton, A. (2018). Learning progression toward a measurement concept of fractions. International Journal of STEM Education, 5, 27 https://doi.org/10.1186/s40594-018-0119-2.
Article Google Scholar
-
Zhao, X., Van den Heuvel-Panhuizen, M., & Veldhuis, M. (2016). Teachers' use of classroom assessment techniques in primary mathematics education – An explorative study with six Chinese teachers. International Journal of STEM Education, 3, 19 https://doi.org/10.1186/s40594-016-0051-2.
Article Google Scholar
Download references
Acknowledgments
Many thanks to Jeffrey E. Froyd for his careful review and detailed comments on an earlier version of this editorial that help improve its readability and clarity. Thanks also go to Marius Jung for his valuable feedback.
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Reprints and Permissions
About this article
Cite this article
Li, Y., Schoenfeld, A.H. Problematizing teaching and learning mathematics as "given" in STEM education. IJ STEM Ed 6, 44 (2019). https://doi.org/10.1186/s40594-019-0197-9
Download citation
-
Received:
-
Accepted:
-
Published:
-
DOI : https://doi.org/10.1186/s40594-019-0197-9
Keywords
- Design-based learning
- Making sense
- Mathematics
- Project-based learning
- Sense making
- STEM education
Nature Of Mathematics Education Pdf
Source: https://stemeducationjournal.springeropen.com/articles/10.1186/s40594-019-0197-9
Posted by: riverahiscriand68.blogspot.com

0 Response to "Nature Of Mathematics Education Pdf"
Post a Comment